电子设备更快计算、更小尺寸和更低功耗需求的不断增长，导致半导体器件的尺寸急剧减小。这个过程已经导致电子器件特性需要考虑量子效应，其中一种便是量子隧穿效应。因此，在设计半导体器件过程中必须要考虑隧穿效应，也就需要采用和考虑不同类型的隧穿模型来刻画其中隧穿效应。

量子隧穿效应

隧穿（Tunneling）是一种量子效应，是微观粒子波动性的体现。在经典力学中，粒子的能量必须要大于势垒的高度才能穿过去。而在量子力学中，即使粒子的能量低于势垒的高度，粒子也有一定的概率穿透过去。

WKB近似

Wiki

WKB近似以三位物理学家格雷戈尔·文策尔、汉斯·克喇末和莱昂·布里渊姓氏字首命名(Wentzel, Kramers, and Brillouin, WKB)。于1926年，他们成功地将这方法发展和应用于量子力学。不过早在1923年，数学家哈罗德·杰弗里斯就已经发展出二阶线性微分方程的一般的近似法。薛定谔方程也是一个二阶微分方程。可是，薛定谔方程的出现稍微晚了两年。三位物理学家各自独立地在做WKB近似的研究时，似乎并不知道这个更早的研究。所以物理界提到这近似方法时，常常会忽略了杰弗里斯所做的贡献。这方法在荷兰称为KWB近似，在法国称为BWK近似，只有在英国称为JWKB近似。

一维的薛定谔方程 $\left[ \frac{\hbar^{2} }{2 m} \frac{d^2}{dx^2} + V(x) \right ] \psi = E\psi$ 可以改写成

\frac{d^{2}\psi}{dx^{2}} + k^{2}(x) \psi = 0

其中

k(x) = \sqrt{\frac{2m}{\hbar^{2}}(E-V(x))} \quad if\, E > V \\ k(x) = i \sqrt{\frac{2m}{\hbar^{2}}(V(x)-E)} = i \kappa(x) \quad if\, E < V \\

如果 $k$ 是一个常数，那么方程的解为 $\psi=e^{\pm i k x}$ 。如果 $k$ 不再是常数，那么解可以写成下面的形式

\psi = e^{i u(x)}

将其倒代入薛定谔方程，可以得到 $u(x)$ 的方程

i u''(x) - u'(x) + k^{2}(x) = 0

通过逐次逼近的方法对其进行近似，我们假定零阶近似为

u_{0} = \pm \int_{a}^{b} k(x) dx

那么解的逼近过程可以写成

u_{n} = \pm \int_{a}^{b} \sqrt{k^{2}(x) + i u^{''}_{n-1}(x)} dx

其中一阶近似可以写成

u_{1} = \pm \int_{a}^{b} \sqrt{k^{2}(x) + i u^{''}_0 (x)} dx \\ = \pm \int_{a}^{b} k(x) \sqrt{1 \pm i\frac{k'(x)}{k^{2}(x)}} dx \\ \approx \int_{a}^{b} \left[ \pm k(x) + \frac{i}{2} \frac{k'(x)}{k(x)} \right] dx \\ = \pm \int_{a}^{b} k(x) dx + \frac{i}{2} \ln[k(x)] + C

当 $|k'| \ll k^{2}$ , 第二项可以近似为零，从而保证了一阶近似的有效性。那么，波函数可以写成

\psi = \frac{1}{k(x)} \exp\left[ \pm i \int_{a}^{b} k(x)dx \right]

当波函数归一化后，常数 $C$ 可以忽略。

隧穿概率

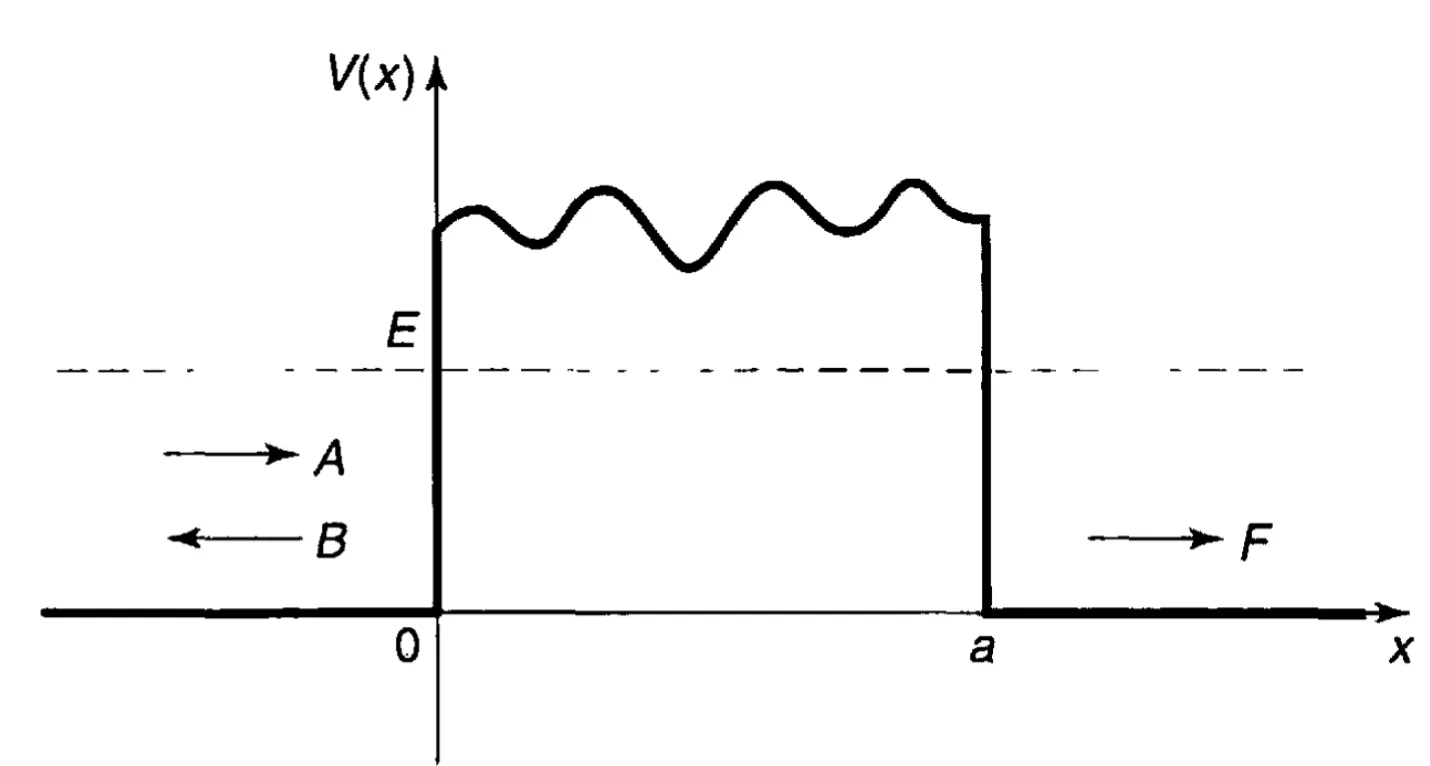
考虑微观粒子（如电子）隧穿过上图的一个任意势，WKB近似可以给出它们的波函数解:

(1) $x< 0$

\psi = A e^{i k x} + B e^{-ikx}

(2) $0 \leq x \leq a$

\psi = \frac{C}{\sqrt{|k(x)|}} \exp \left[i\int_{0}^{x} k(x') dx' \right] + \frac{D}{\sqrt{|k(x)|}} \exp \left[- i \int_{0}^{x} k(x') dx' \right]

(3) $x > 0$

\psi = F e^{-ikx}

如上图所示，我们可以期望在 $x\in[0,a]$ 波函数式指数衰减的，势垒越高，系数 $C$ 越小。由于波函素的连续性，我们可以估计隧穿概率为

T_{\mathrm{WKB}} = \frac{|F|^2}{|A|^2} \approx \exp \left[- 2\int_{0}^{a} |k(x)| dx \right]

其中 $k(x)$ 是粒子在势垒内虚拟的波矢量。

注

这是基于WKB近似得到的结果，和真实准确的进行对比。例如，对于势垒为常数，即 $V(x) = V_{0}$ ，可以准确计算得到隧穿概率：

T_{\mathrm{exact}} = \left[ 1 + \frac{V_{0}^2}{4E(V_{0}-E)} \sinh^2 (|k|a) \right] \approx \left( \frac{16}{ 3+ V_{0}/E} \right) e^{-2|k|a}

而WKB近似下的隧穿概率：

T_{\mathrm{WKB}} = e^{-2i|k|a}

所以WKB近似下可以很好的计算得到重现出当指数项占主导地位的隧穿概率，而且计算公式较为简单。

参考资料

[1] The WKB approximation.

[2] Chapter 9: The WKB Approximation.

目录

量子隧穿效应

WKB近似

隧穿概率

参考资料